一直到現在為止，我們在物理中所探討的物體移動，大部分都將物體假設成位於質心的一個質點進行移動。這樣的假設或許在很多情況下影響不大，但在一些時候，這樣的假設就太過馬虎了。

旋轉就是一個例子：當一顆輪胎在路面上滾動時，你應該不會想要將它假設成一個位於輪心、沿著路面平移的質點吧！因此，在接下來的幾個章節裡，我們要將之前所學的概念推廣出去，理解轉動中物體的一些物理特性。

轉動的位置

首先，我們要來探討的是物體旋轉時的旋轉位置—角位置（Angular Position），通常以希臘字母 $\theta$ 表示。角位置的概念相當簡單，它描述著一個旋轉中的物體轉了幾圈、轉到哪裡。在下圖中，我們將圓心水平向右處定為零角位置，也就是轉動過程中的原點。

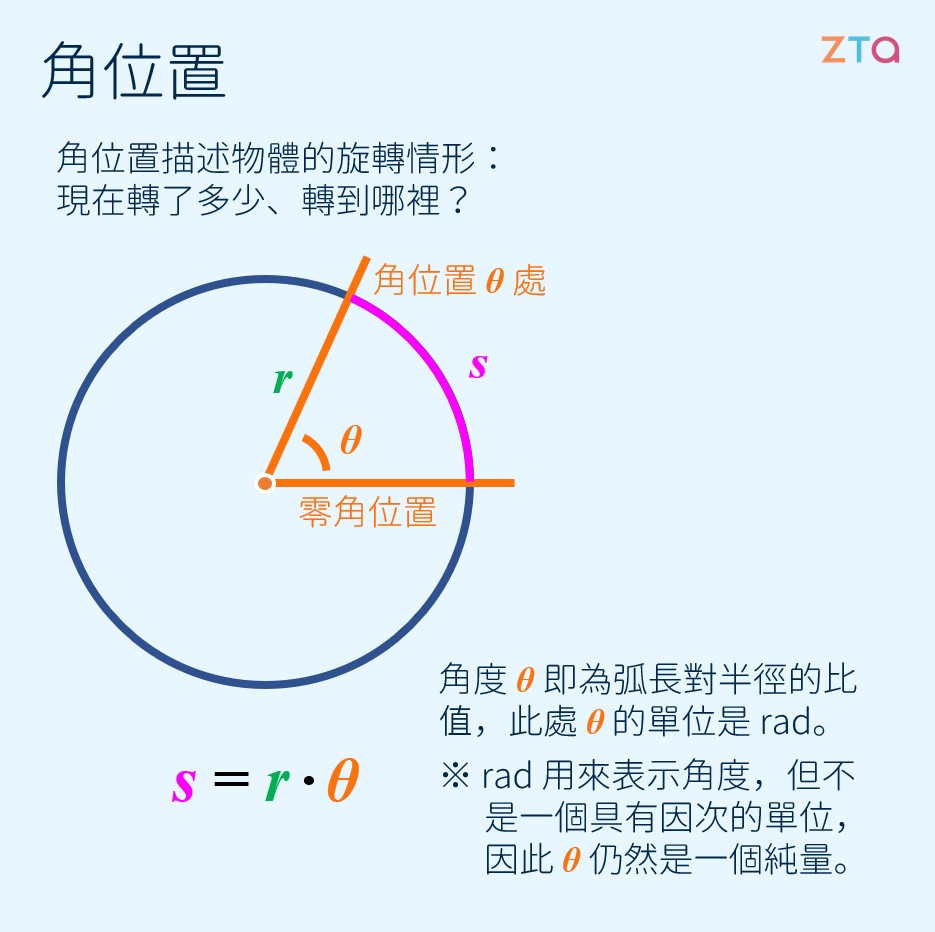
在物體開始旋轉後的某個時刻，物體從零角位置轉了幾度，就是該時刻物體的角位置。若我們像圖中一樣將物體畫作一個半徑為 $r$ 的圓，我們便可寫出這樣的關係式：

$s = r\cdot \theta$

又或者：

$\theta = \frac{s}{r}$

如同我們在式子中所見，角度 $\theta$ 其實就是弧常對半徑的比值。此處，角度的單位是 rad，或者，我們可以稱其為弧度。值得注意的一點是，rad 是一個純數字，不像其他物理單位（例如：公尺）一樣具有實際的因次意義。

既然同樣表示角度，那麼 rad 跟我們所熟知的度（°）間是什麼樣的關係呢？我們都知道繞圓一圈是 $360 ^\circ$，而我們也知道圓周長是 $2\pi r$，再看看上面的式子，我們可以得到下列兩的等式：

$\theta = 360^\circ= \frac{s}{r}$

將圓周長的 $s = 2\pi r$ 代入，我們便能得到：

$360^\circ= 2\pi$

從位移到角位移

在討論直線運動時，我們將運動前後的位置差異稱作位移。換句話說，假設剛開始物體所在的位置是 $x_i$，運動結束時所在位置是 $x_f$，那麼位移 $\Delta x$ 就會是：

$\Delta x = x_f - x_i$

用這種「後減前」的模式，我們得出了在運動過程中物體的位移。同樣地，在計算角速度時，我們也能以這種「後減前」的模式來計算轉動的量。假設起初物體的角位置是 $\theta_i$，轉動結束時，物體的角位置是 $\theta_f$，那麼在這個轉動的過程，物體的角位移 $\Delta \theta$ 就是：

$\Delta \theta = \theta_f - \theta_i$

角速度與角加速度

平均角速度

在速度的章節中，我們將速度定義為「單位時間內的位移量」。依據這個定義，假設我們已知運動過程中的位移 $\Delta x$，以及其所花的時間 $\Delta t$，我們可以這樣求得平均速度 $v_{avg}$：

$v_{avg} = \frac{\Delta x}{\Delta t}$

其中，下標的 $avg$ 代表英文中的 average，表示平均。我們可以將這個計算平均速度的過程推廣到角速度上—假設已知轉動過程中的角位移為 $\Delta \theta$，以及其所花的時間 $\Delta t$，我們可以求得平均角速度 $\omega_{avg}$：

$\omega_{avg} = \frac{\Delta \theta}{\Delta t}$

所謂的角速度（Angular Velocity），不就是轉動的速度罷了！我們可以用速度的概念來思考：同樣的時間內走得越遠，速度越大；同樣的距離下時間越少，速度越大。角速度也是一樣的，相同時間內轉得越多，角速度越大；轉相同的角度時所需時間越少，角速度越大。

瞭解角速度後，我們便能計算物體旋轉時其邊緣的切線速度。還記得嗎？速度是單位時間下走的距離，而角速度是單位時間下轉了多少。這兩者之間要怎麼建立起數字上的關係來呢？可以在此處稍微思考一下，再繼續往下看。

讓我們回想一下上述介紹角度與弧度的部分。我們知道，如果要求得圓周上一點在轉動時所劃過的路徑長，我們可以用 $s = r\cdot \theta$ 的關係來解。而我們也知道，單位時間下物體走過的距離就是其速率。而此處，物體走過的距離是圓周上的弧長 $s$。是不是看出什麼關係來了呢？

再重複一次，現在所要求得的，是切線速度和角速度間的關係。而我們知道切線速度 $v = s/\Delta t$。其實至此，切線速度和角速度間的關係已經被建立起來了，因為：

$v = \frac{s}{\Delta t} = \frac{r\cdot \Delta\theta}{\Delta t}$

而：

$\frac{\Delta\theta}{\Delta t} = \omega$

將第二個式子代入第一個式子，我們便能得到關係式：

$v = r\omega$

平均角加速度

在開始探討平均角加速度之前，我們可以先花費一些時間複習一下加速度。在之前的章節裡，我們將加速度定義為「單位時間內的速度變化量」。現在，假設有一個物體的加速度為 $15m/s^2$，那麼代表什麼呢？

這代表了該物體的速度正在以每秒 $15m/s$ 的變化在改變：假設現在正以 $13m/s$ 的速度運動，那麼下一秒它就會以 $28m/s$ 的速度運動；假設它現在正以 $-7m/s$ 的速度運動，那麼下一秒它就會以 $8m/s$ 的速度運動。

而加速度的單位是 $m/s^2$，也告訴著我們它本質上的意義。通常，我們可以將單位裡的除號「$/$」想成是「每…改變…」。速度的單位是 $m/s$，表示「每秒改變幾公尺」。而加速度的單位是 $m/s^2$，也就是 $(\frac{m}{s})/s$，我們可以將其想成是「每秒改變了 每秒幾公尺」—這也符合了加速度的定義：單位時間內的速度變化量。

既然加速度是單位時間內的速度變化量，那麼角加速度就是單位時間內的角速度變化量了！依據這樣的定義，假設一物體的角速度在 $\Delta t$ 的時間內變化了 $\Delta \omega$，其平均角加速度 $\alpha_{avg}$ 為：

$\alpha_{avg} = \frac{\Delta\omega}{\Delta t}$

接著，如同剛才提到角速度與切線速度的關係，角加速度與切線加速度間的關係為：

$a = r\alpha$

其中，$r$ 是旋轉中物體的半徑。注意不要將符號搞混！式子中的英文字母 $a$ 代表的是直線的加速度，而式子中的希臘字母 $\alpha$（讀作：alpha）代表的是轉動過程中的角加速度。

微積分的觀點

之前，我們曾用一整個章節介紹位移、速度、加速度間的數學關係。速度是位移除以時間，加速度是速度除以時間，因此三者間的關係就在於時間乘除。而我們知道，這樣的關係可以微分和積分的形式來表達。

既然位移、速度、加速度間存在這樣的微分與積分的關係，那麼角位移、角速度、角加速度間勢必也存在著這樣的關係。長話短說，角速度是角位移對時間的微分，而角加速度是角速度對時間的微分。

但究竟如何抵達這樣的結論呢？剛才我們所計算的角速度，都是一段時間內的平均角速度。然而，如果我們將時間的採樣區域縮小，小到趨近於 0，那麼我們的計算結果便會是瞬時角速度：

$\omega = \lim_{\Delta t\to 0}\frac{\Delta \theta}{\Delta t} = \frac{d\theta}{dt}$

同樣地，若將平均角加速度的時間採樣區域縮小到趨近於 0，那麼計算的結果便會是瞬時角加速度：

$\alpha = \lim_{\Delta t\to 0}\frac{\Delta\omega}{\Delta t} = \frac{d\omega}{dt}$

微分的相反就是積分，因此我們也可以將剛剛所得到的結論倒過來寫—角速度是角加速度對時間的積分，而角位移是角速度對時間的積分：

$\Delta \omega = \int \alpha\cdot dt$

$\Delta \theta = \int \omega\cdot dt$