三角函數的定義
三角函數,是人們用來表示三角形上邊長與邊長之間關係的函數。當我們觀察一個直角三角形時,我們可以將各個函數定義作如下(adj為鄰邊;opp為對邊;hyp為斜邊):
sin(θ)=hypopp , cos(θ)=hypadj
csc(θ)=opphyp , sec(θ)=adjhyp
tan(θ)=adjopp , cot(θ)=oppadj
利用這些定義,我們可以衍伸出一些式子,表達不同三角函數間的關係:
tan(θ)=cos(θ)sin(θ) , cot(θ)=sin(θ)cos(θ)
sec(θ)=cos(θ)1 , csc(θ)=sin(θ)1
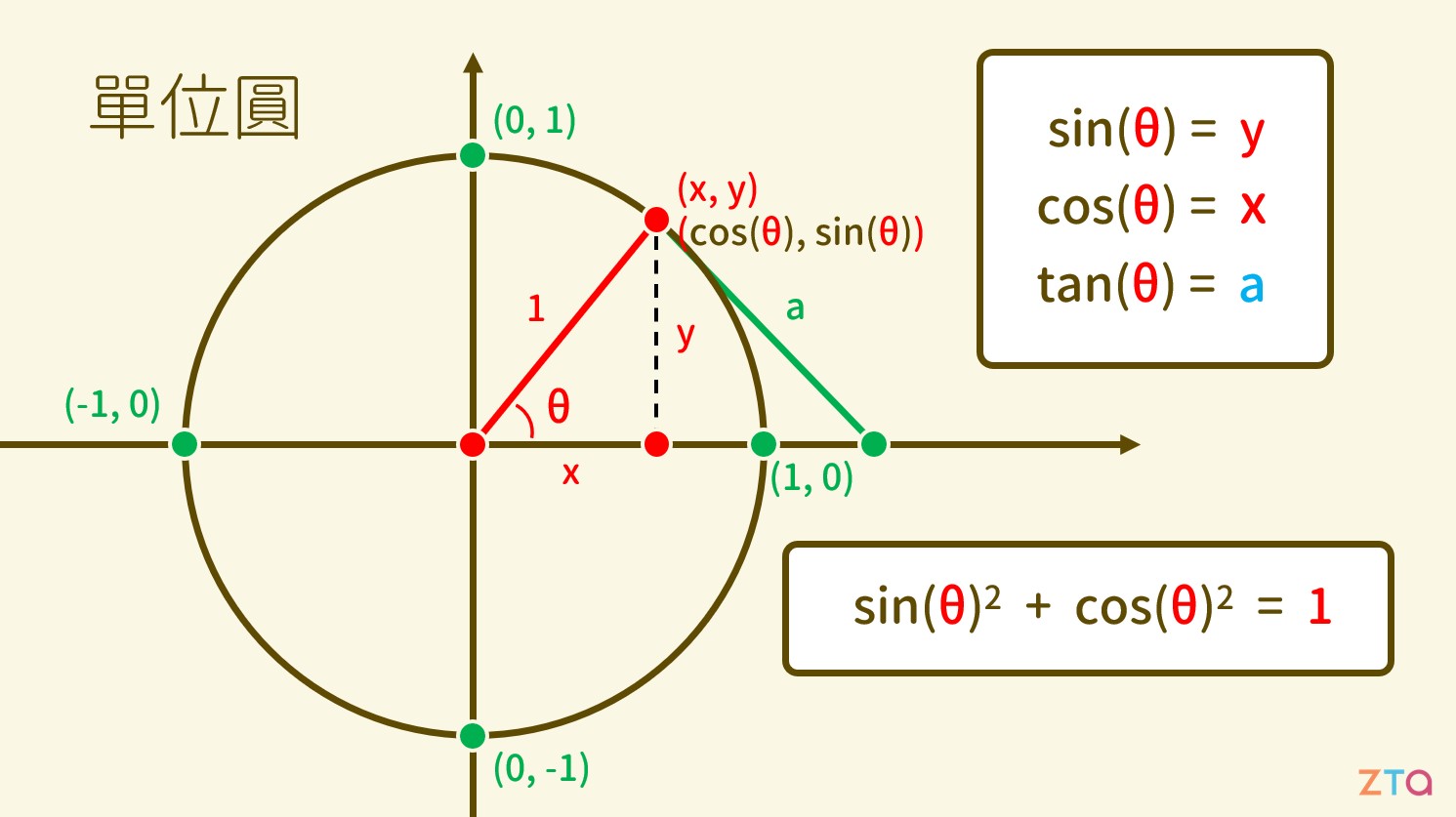
在單位圓中,我們可以將這些函數所對應的值在圖形上表示出來,也就是:
sin(θ)=y , cos(θ)=x
而 tan(θ) 即為半徑 r 的斜率。
衍伸的公式
將 cos 與 sin 的定義進行整理,我們可以得到:
sin2θ+cos2θ=1
⇒sin2θ=(1+cosθ)(1−cosθ)
⇒cos2θ=(1+sinθ)(1−sinθ)
接著一樣很重要的是角度加減的公式:
sin(α+β)=sinα⋅cosβ+cosα⋅sinβ
sin(α−β)=sinα⋅cosβ−cosα⋅sinβ
cos(α+β)=cosα⋅cosβ−sinα⋅sinβ
cos(α−β)=cosα⋅cosβ+sinα⋅sinβ
藉由 sin 與 cos 的加減公式,我們可以得到:
tan(α+β)=1−tanα⋅tanβtanα+tanβ
tan(α−β)=1+tanα⋅tanβtanα−tanβ
若將 α 和 β 代入相同的值,我們便能得到兩倍角公式:
sin(2θ)=2⋅sinθ⋅cosθ
cos(2θ)=cos2θ−sin2θ
tan(2θ)=1−tan2θ2⋅tanθ
將上述公式代入不同符號並整理,可得半角公式:
sin(2θ)=±√21−cosθ
cos(2θ)=±√21+cosθ
tan(2θ)=±1+cosθsinθ
最後是 sin 與 cos 的加減公式:
sinα+sinβ=2⋅sin(2α+β)⋅cos(2α−β)
sinα−sinβ=2⋅sin(2α−β)⋅cos(2α+β)
cosα+cosβ=2⋅cos(2α−β)⋅cos(2α+β)
cosα−cosβ=2⋅sin(2α−β)⋅sin(2α+β)
幾何上的運用
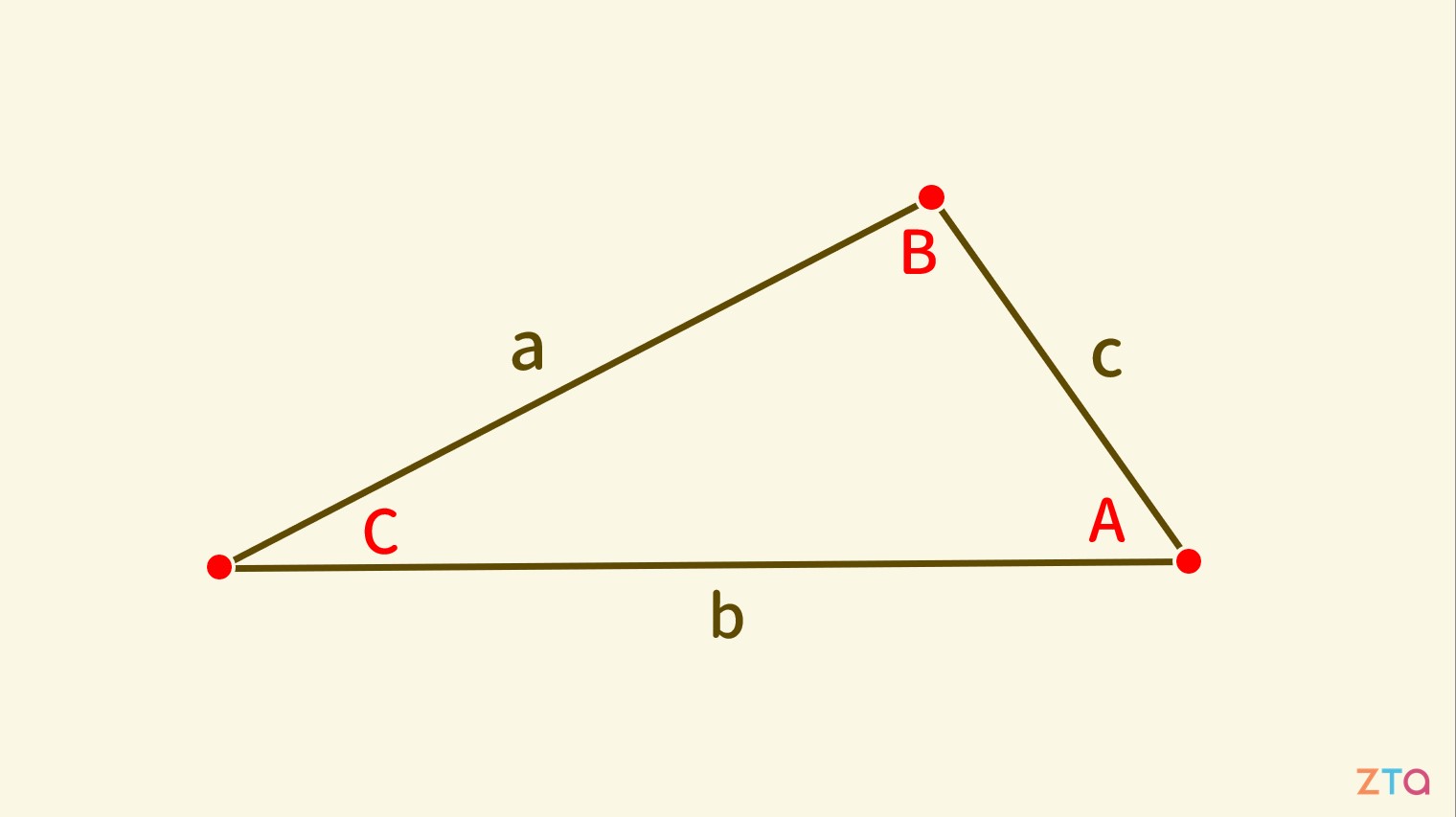
當我們有一個三角形,邊長與角度如上圖所示時,則面積會等於一半的兩邊乘上夾角的 sin 值:
Area=21⋅a⋅b⋅sin(∠C)
三邊長與對角的關係呈:
sin∠Aa=sin∠Bb=sin∠Cc
任意一邊長與另外兩邊的關係為:
c2=a2+b2−2⋅a⋅b⋅cos∠C
若我們將 ∠C 以 90度 帶入,則:
let∠C=90∘
⇒cos∠C=0
⇒c2=a2+b2
即得畢氏定理。

