三角函數公式整理｜學呀

三角函數公式整理

加至書籤

# 三角函數的定義

三角函數，是人們用來表示三角形上邊長與邊長之間關係的函數。當我們觀察一個直角三角形時，我們可以將各個函數定義作如下（$adj$為鄰邊；$opp$為對邊；$hyp$為斜邊）：
$$ \sin(\theta) = \frac{opp}{hyp} \text{ , } \cos(\theta) = \frac{adj}{hyp} $$
$$ \csc(\theta) = \frac{hyp}{opp} \text{ , } \sec(\theta) = \frac{hyp}{adj} $$
$$ \tan(\theta) = \frac{opp}{adj}  \text{ , } \cot(\theta) = \frac{adj}{opp} $$

利用這些定義，我們可以衍伸出一些式子，表達不同三角函數間的關係：
$$ \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}  \text{ , } \cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)} $$
$$ \sec(\theta) = \frac{1}{\cos(\theta)}  \text{ , } \csc(\theta) = \frac{1}{\sin(\theta)} $$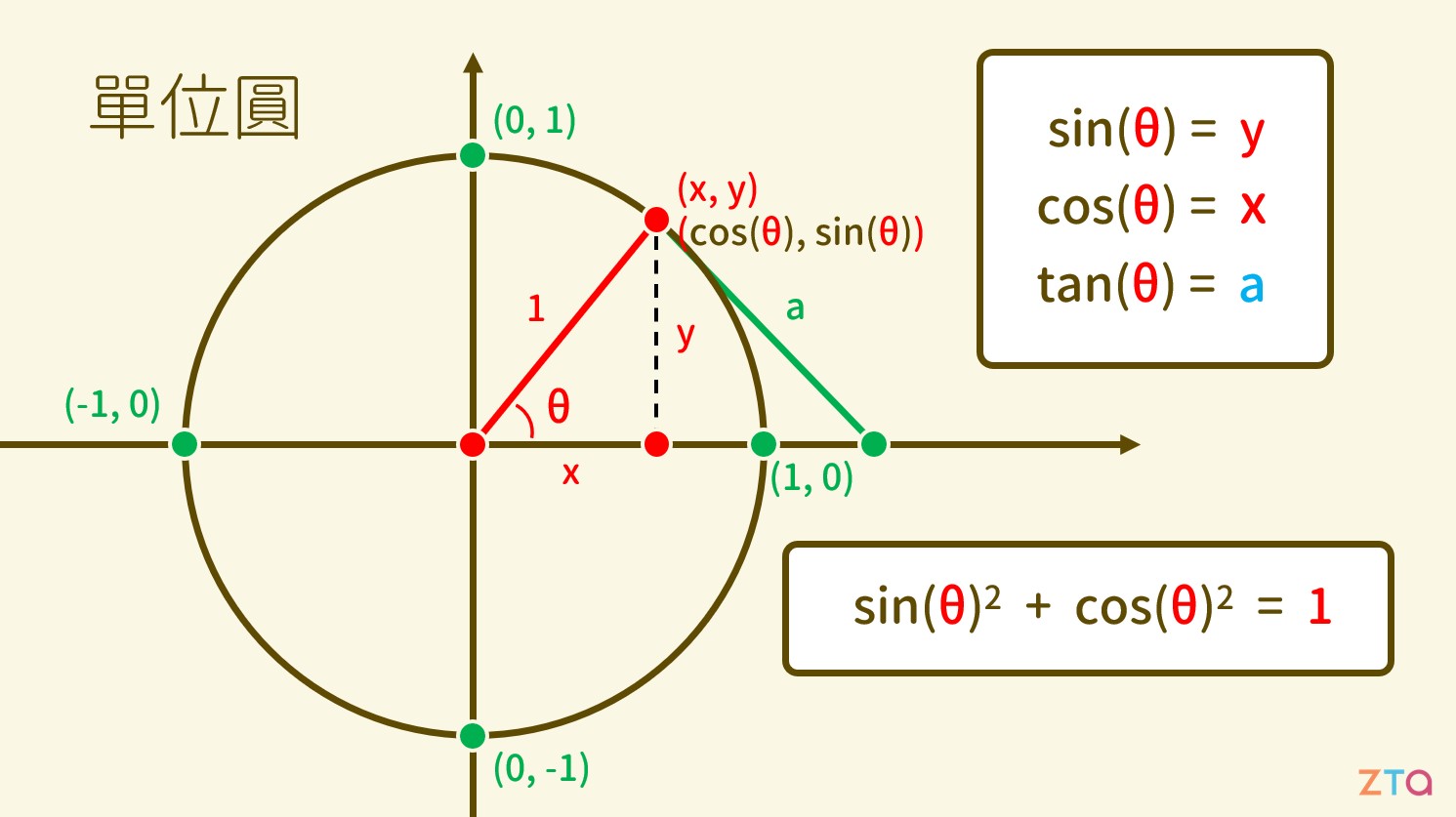

![三角函數與單位圓形｜基礎數學｜學呀](https://raw.githubusercontent.com/zetria-org/content/main/images/97jyr5ryh.jpg)

在單位圓中，我們可以將這些函數所對應的值在圖形上表示出來，也就是： 
$$ \sin(\theta) = y \text{ , } \cos(\theta) = x $$
而 $\tan(\theta)$ 即為半徑 $r$ 的斜率。

# 衍伸的公式

將 $\cos$ 與 $\sin$ 的定義進行整理，我們可以得到：
$$ \sin^2 \theta + \cos^2\theta = 1 $$
$$  \Rightarrow \sin^2\theta = (1+\cos\theta)(1-\cos\theta) $$
$$  \Rightarrow \cos^2\theta = (1+\sin\theta)(1-\sin\theta) $$

接著一樣很重要的是角度加減的公式：
$$ \sin(\alpha+\beta) = \sin\alpha \cdot \cos\beta +\cos\alpha \cdot \sin\beta $$
$$ \sin(\alpha-\beta) = \sin\alpha \cdot \cos\beta -\cos\alpha \cdot \sin\beta $$
$$ \cos(\alpha+\beta) = \cos\alpha \cdot \cos\beta -\sin\alpha \cdot \sin\beta $$
$$ \cos(\alpha-\beta) = \cos\alpha \cdot \cos\beta +\sin\alpha \cdot \sin\beta $$

藉由 $\sin$ 與 $\cos$ 的加減公式，我們可以得到：
$$ \tan(\alpha+\beta) = \frac{\tan\alpha+\tan\beta}{1-\tan\alpha \cdot \tan\beta} $$
$$ \tan(\alpha-\beta) = \frac{\tan\alpha-\tan\beta}{1+\tan\alpha \cdot \tan\beta} $$

若將 $\alpha$ 和 $\beta$ 代入相同的值，我們便能得到兩倍角公式：
$$ \sin(2\theta) = 2\cdot \sin\theta \cdot \cos\theta $$
$$ \cos(2\theta) = \cos^2\theta - \sin^2\theta $$
$$ \tan(2\theta) = \frac{2 \cdot \tan\theta}{1-\tan^2\theta} $$

將上述公式代入不同符號並整理，可得半角公式：
$$ \sin(\frac{\theta}{2}) = \pm \sqrt{\frac{1-\cos\theta}{2}} $$
$$ \cos(\frac{\theta}{2}) = \pm \sqrt{\frac{1+\cos\theta}{2}} $$
$$ \tan(\frac{\theta}{2}) = \pm\frac{\sin\theta}{1+\cos\theta} $$

最後是 $\sin$ 與 $\cos$ 的加減公式：
$$ \sin\alpha + \sin\beta = 2\cdot \sin(\frac{\alpha+\beta}{2})\cdot \cos(\frac{\alpha-\beta}{2}) $$
$$ \sin\alpha - \sin\beta = 2\cdot \sin(\frac{\alpha-\beta}{2})\cdot \cos(\frac{\alpha+\beta}{2}) $$
$$ \cos\alpha + \cos\beta = 2\cdot \cos(\frac{\alpha-\beta}{2})\cdot \cos(\frac{\alpha+\beta}{2}) $$
$$ \cos\alpha - \cos\beta = 2\cdot \sin(\frac{\alpha-\beta}{2})\cdot \sin(\frac{\alpha+\beta}{2}) $$

# 幾何上的運用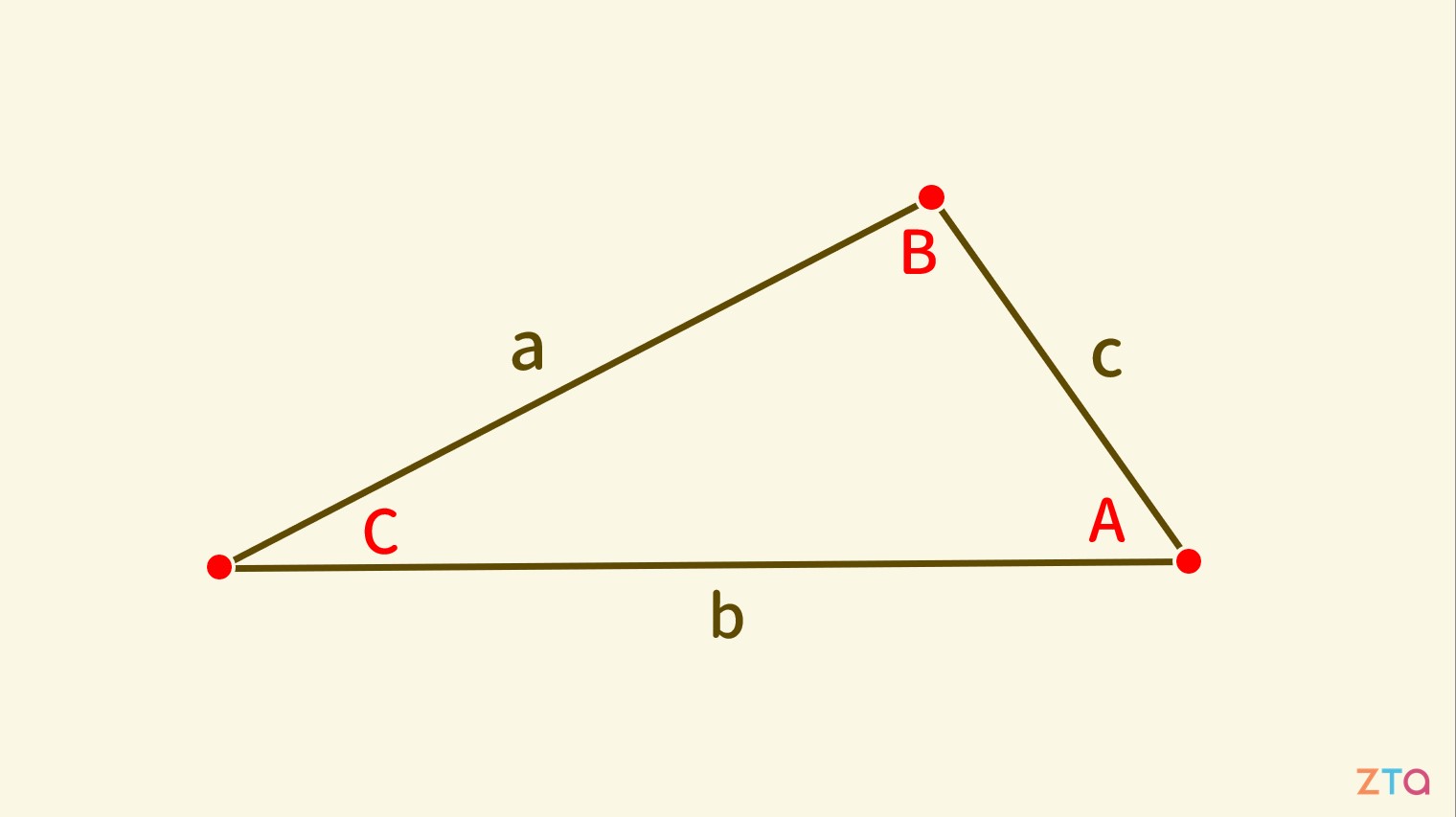

![三角函數在幾何上的運用｜正弦、餘弦定理｜學呀](https://raw.githubusercontent.com/zetria-org/content/main/images/ikswp9qwx.jpg)

當我們有一個三角形，邊長與角度如上圖所示時，則面積會等於一半的兩邊乘上夾角的 $\sin$ 值：
$$ \text{Area} =\frac{1}{2}\cdot a\cdot b\cdot \sin(\angle C) $$
三邊長與對角的關係呈：
$$ \frac{a}{\sin\angle A} = \frac{b}{\sin\angle B} = \frac{c}{\sin\angle C} $$
任意一邊長與另外兩邊的關係為：
$$ c^2 = a^2 + b^2 - 2\cdot a\cdot b\cdot \cos\angle C $$
若我們將 $\angle C$ 以 90度 帶入，則：
$$ let \angle C = 90^{\circ} $$
$$ \Rightarrow \cos\angle C = 0 $$
$$ \Rightarrow c^2 = a^2 + b^2 $$ 
即得畢氏定理。

複製內容