尚未建立名稱
能量:0
我的帳號中心
問 學Bot 任何問題!
首頁&搜尋
最愛&收藏
所有課程
分享資源
帳號設定
關於學呀
線上募款
虎克定律
編輯章節
EDU-MD
Google 教室
加至書籤
# 虎克定律  ## 力如伸長 想像一下這個畫面:在你手中有一個原子筆中的彈簧,在沒有壓扁的情況之下,假設你施了兩倍的力,彈簧的壓縮量會不會變成原本的兩倍呢?答案是會的! 彈簧只要在**彈性限度**之內,長度的變化量會與受力的大小成正比。彈性限度是彈簧可以正常運作的受力範圍:想像一下剛剛那條彈簧,如果非常用力地將其往兩側拉扯,將其拉成一條鋼絲,那這條彈簧就壞掉了!在一條超越彈性限度後,會永久地受損,再也不能正常運作。 剛剛講到的,彈簧的長度的變化量會與受力的大小成正比,正是虎克定律中所提到的。讓我們用下面這張圖來解釋: 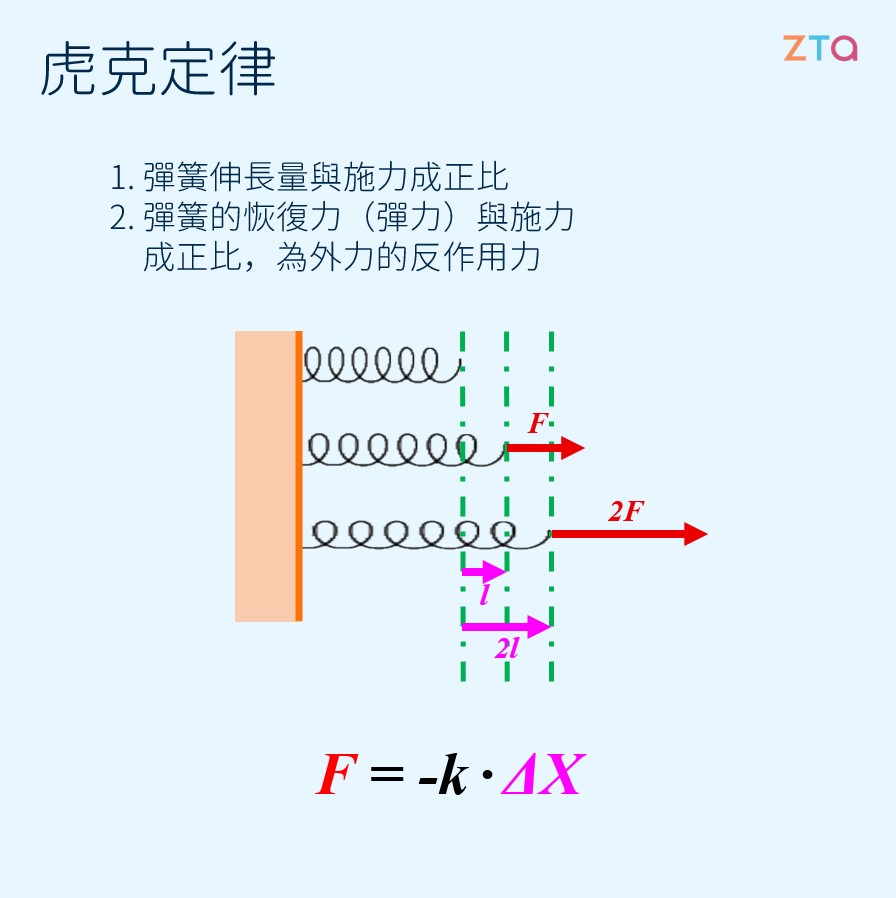 在我們將彈簧拉伸或者壓縮時,彈簧會產生一個**對抗形變**的力,這個力可以看成是外力的反作用力。如上圖中所示,彈力 $F$ 與彈簧的長度變化量 $\Delta X$ 成正比,以一彈力係數作為其比例係數: $$F = -k\cdot \Delta X$$ 之所以在式子中有一個負號,是因為彈力 $F$ 所作用的方向與彈簧的長度變化量 $\Delta X$ 方向相反。在計算時,只須注意力的方向,就沒問題了哦!不同的彈簧,具有不同的彈力係數 $k$。$k$ 的值越大,代表該彈簧越硬,越難拉伸或壓縮,連帶地,在相同形變量下該彈簧也會具有較大的彈力。 當我們在退動彈簧時,就好像將能量儲存到彈簧中一樣,在我們放開手之後,彈簧便會藉由對外界施力把我們儲存的能量釋放出來,這種儲存的能量稱為**彈力位能**,在[這個章節](/view/7a08bdc157?subj=physics)中我們有更深入的討論。
複製內容