尚未建立名稱
能量:0
我的帳號中心
問 學Bot 任何問題!
首頁&搜尋
最愛&收藏
所有課程
分享資源
帳號設定
關於學呀
線上募款
彈力位能
編輯章節
EDU-MD
Google 教室
加至書籤
# 彈簧的能量  ## 彈性位能是什麼 我們知道,若是將物體放置到高處,在沒有東西支撐的情況下,物體會自己落下。而在落下的過程中,物體的動能不斷地增加,這是因為物體本來的重力位能被轉換成動能。 同樣的道理,如果我們今天將一個木塊推向彈簧,使得彈簧被推離平衡位置之後放開手,我們可以看到木塊被彈簧彈出去了。木塊的速度發生改變,因而產生了動能。而這些動能是哪裡來的呢? 沒錯,就是從一開始的彈簧來的。在我們推動彈簧的同時,便是在將能量儲存到彈簧中,等到手放開木塊的那一剎那,彈簧所儲存的**彈力位能**便開始被轉換為物體的動能。同樣關係到彈性位能的還有橡皮筋的拉伸、鬆緊帶的縮放、彈弓的彈射等。 ## 用作功看位能 讓我們試著直覺地思考,彈簧在什麼情況下不帶有任何的彈性位能?這個問題簡單明瞭,任何不懂物理的人都能回答:在彈簧沒有被壓縮或伸展的情況下。因此,讓我們從彈簧平衡的時候開始討論。 首先,彈簧在平衡時是沒有彈力位能的。而當我們開始壓縮彈簧,彈力位能也就隨之增加。現在一個很重要的問題來了:這些增加的位能是從何而來的?這個的答案也很簡單:因為是我們用手推動彈簧,表示**彈力位能是源於手對彈簧的作功**。 在知道了這一點後,我們便可以計算彈簧的彈力位能了。我們先來複習一下[作功](/view/14ad0a00e6?subj=physics)的基本定義: $$W = F\cdot s$$ 其中,$F$ 代表著所施的力,而 $s$ 代表著施力所造成的位移。這裡需要注意,因為施力所造成的位移,因此在求位移時,必須求得的是與施力平行的位移,才能得到正確的結果。 上述這個式子只能在施力相等的情況下使用,也就是說,在位移的過程中,物體所受的力量大小必須保持在同一個值。然而,我們可以思考一下,根據[虎克定律](/view/656cbe3196?subj=physics),手對彈簧的施力隨著位移而改變: $$ F = -k\cdot \Delta X$$ 這也表示,在彈簧壓縮的過程中,施力並不保持一定,因此我們不能使用上面作功的式子。不過,只要我們將該式寫作積分的形式,就可以順利地使用了!這是因為積分的過程中,我們將位移切作無限個小區塊,在各個小區塊內的施力都保持相等,因此可以用來計算作功。 $$W = \int F \cdot ds$$ 另外,彈簧的位移 $s$ 就是虎克定律中的 $\Delta X$,以下寫作 $X$。帶入虎克定律的式子後,我們可以得到: $$W = \int (k\cdot X)\cdot dX$$ $$ = \frac{1}{2}kX^2$$ 因此,我們便得到彈力位能 $U$ 的公式,其中,$k$ 代表彈簧的彈力係數,而 $X$ 代表彈簧末端最後與平衡位置的距離,即彈簧的壓縮量: $$U = \frac{1}{2}kX^2$$ ## 三角形面積計算位能 物理與數學最美麗的地方在於,我們不需要死背公式也可以學會怎麼計算,將觀念理解的透徹。上面我們使用積分來計算彈力位能,然而,我們只需要將作功的定義理解清出,便可以用圖表來解決。 在具有一些微積分的知識後,我們知道作功其實就是施力對位移的圖形中,函數下方的圖形面積。而因為虎克定律為一個線性函數,我們可以作出下列的圖,利用三角形面積來計算彈力位能: 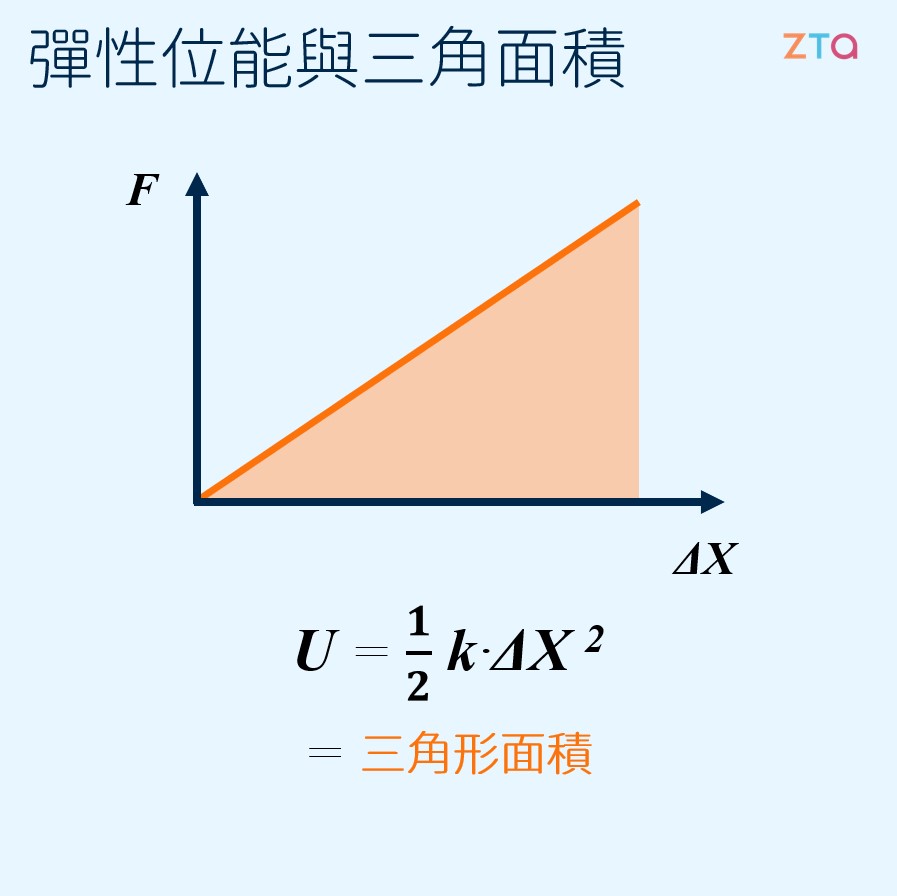 ## 思考彈力位能的公式 在經過了上面的公式推導後,我們得到了萬用的彈力位能公式。只要彈簧遵守虎克定律,並且維持在彈性限度內,其彈力位能: $$U = \frac{1}{2}kX^2$$ 仔細觀察這個公式後,你可能會有疑問:明明是一個簡簡單單的彈簧,我用手輕輕鬆鬆就推動它了,為什麼彈力位能的公式會有 $X^2$?其實,這並不奇怪,我們可以用一點生活經驗去思考: 假設你手上拿著一個有點硬的彈簧,現在,你用食指與拇指想要把彈簧壓扁。剛開始,彈簧只被壓縮一點點時,你會覺得輕鬆而不費力。然而,當你繼續對它施力,彈簧越來越趨近於被壓扁時,你會覺得壓扁彈簧不再輕鬆,而是相當費力的。 沒錯,剛開始壓扁彈簧時,你的手花費不怎麼多的能量在壓縮這個彈簧。當彈簧愈來愈扁,也就是 $X$ 愈來愈大時,你的手需要花費愈來愈多的能量才能壓扁它。因此我們可以合理地推測,彈力位能與伸長量並不單單只是正比關係,而是平方關係—的確,公式正是這樣告訴我們的!
複製內容