常見的轉動慣量｜學呀

常見的轉動慣量

加至書籤

# 常見的轉動慣量

什麼是**轉動慣量**？如同我們在[前一個章節](/physics/321da0a333)所介紹的，轉動慣量所描述的是一個物體的質量與質量的分布情形，藉此來描述它在轉動過程中的動作。轉動慣量（moment of inertia）在轉動力學中相當於移動力學的質量：質量越大，越難推動；轉動慣量越大，越難轉動。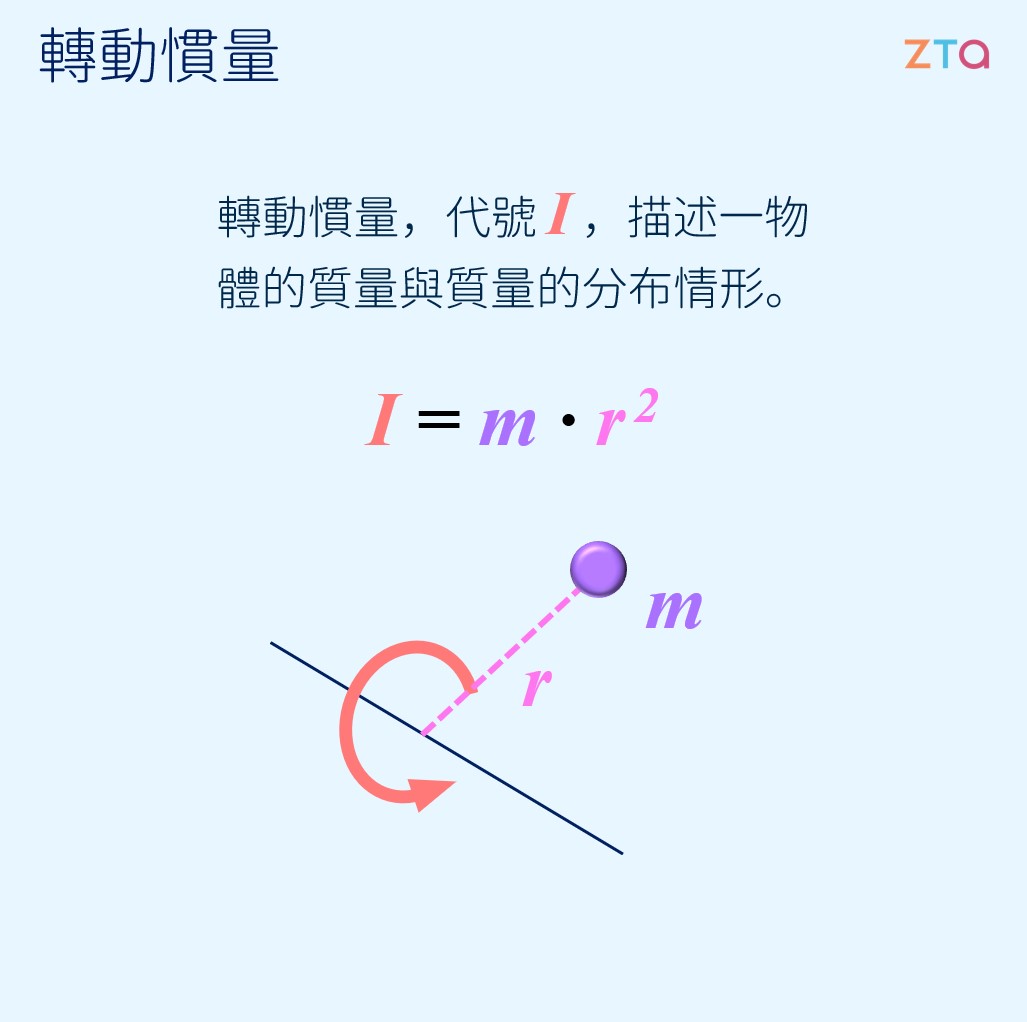

![](https://raw.githubusercontent.com/zetria-org/content/main/images/2h5tr1unf.jpg)

另外，前一個章節中我們也推導了長細棒的轉動慣量。以下，我們再將其推導一次，並且列舉一些常見的轉動慣量計算。

## 長細棒的轉動慣量

當我們要計算一個非質點物體的轉動慣量時，可以將該物體切分成很多的小質點，再將各個質點的轉動慣量加總。在此，以一個長度為 $L$，質量為 $m$ 的細長棒子為例，求出其繞著質心（棒子中點）旋轉時的轉動慣量，如下圖所示：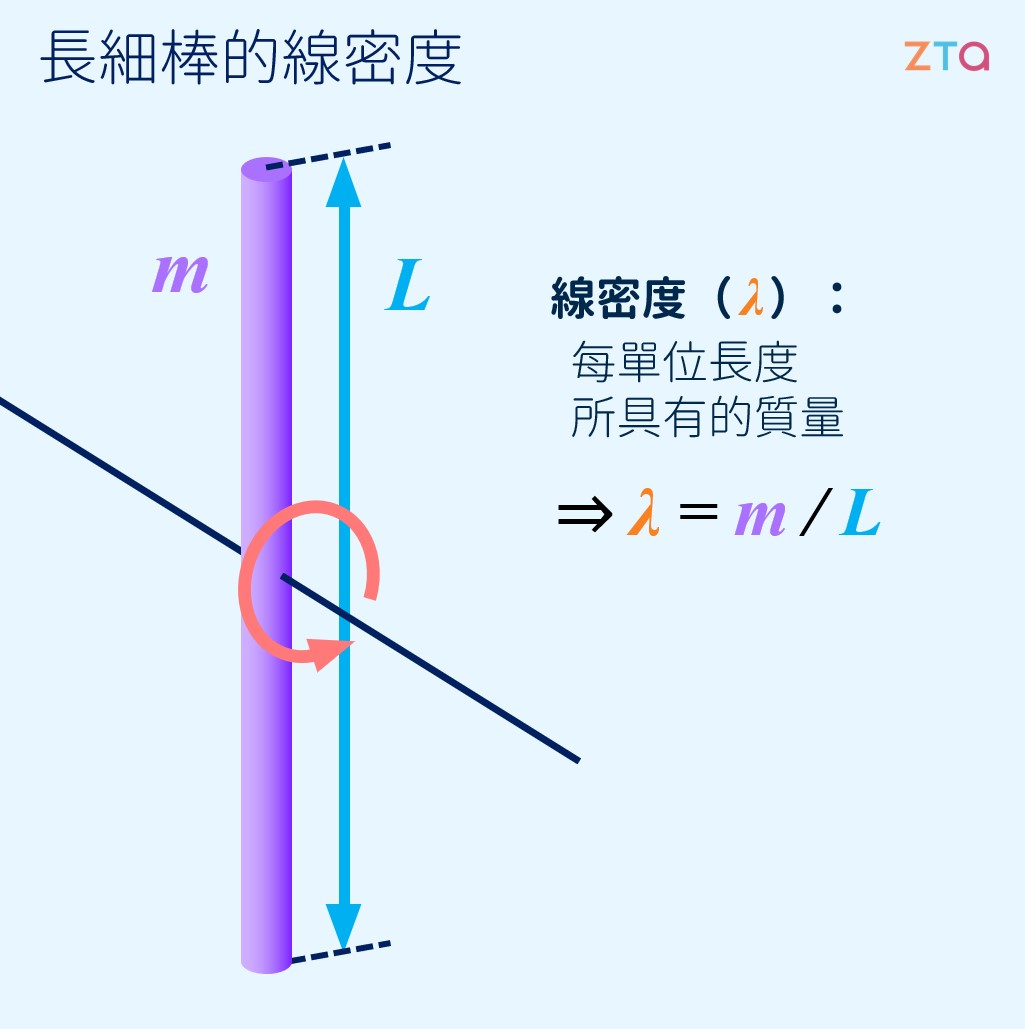

![](https://raw.githubusercontent.com/zetria-org/content/main/images/t3hb1qmed.jpg)

為了解決這個問題，我們先來回想一下，一個質點的轉動慣量 $I = mr^2$，而今天我們所要計算的棒子並非一個質點，因此我們可以將其想像為無限多的小質點，再把這些小質點的轉動慣量加總起來，就是細棒的轉動慣量了。運用一點 **[微積分](/view/2d296cd71a?subj=physics)** 的概念，我們可以把每個小質點的轉動慣量設為 $dI$，並將質量設為 $dm$，便能得到：

$$dI = dm\cdot r^2$$

因為棒子的長度是 $L$，因此兩端距離旋轉中心的距離皆為 $L/2$。也就是說，我們必須將半徑從 $-L/2$ 到 $L/2$ 的小質點都加總起來。因此，我們可以得到這樣的式子：

$$I = \int_{r=-L/2}^{r=L/2}dm\cdot r^2 $$

但是在這裡，我們遇到了一個問題：我們所要計算的式子，是對 $r$ 作積分，但是積分式子裡的變數卻是 $dm$，那要怎麼辦呢？我們可以想辦法將 $dm$ 代換成 $dr$。此時，**線密度**就能派上用場了。線密度，指的就是單位長度上所具有的質量。因此，我們可以將這根棒子的線密度定義為 $\lambda$：

$$\lambda=\frac{m}{L}$$

接著，我們要做的就是把剛剛積分式中的 $dm$ 代換成 $dr$ 了。我們可以思考一下，$dm$ 是一小段長度所具有的質量，而 $dr$ 是每一小段的長度，也就是說，我們可以將兩者與線密度之間建立起關係：

$$ dm = \lambda\cdot dr $$

將以上算式帶入積分式中，即可對 $r$ 做積分：

$$\int_{-L/2}^{L/2} \lambda \cdot dr \cdot r^2=\lambda \frac{1}{3}r^3 \Big\vert_{-L/2}^{L/2} =\lambda \cdot \frac{L^3}{12}$$

最後再將 $\lambda$ 還原回原有條件 $m/L$，就求得了棒子的轉動慣量為：

$$\frac{1}{12}mL^2$$

## 薄圓柱的轉動慣量

敬請期待

## 薄圓盤的轉動慣量

敬請期待

## 實心球體的轉動慣量

敬請期待

複製內容