斜面原理

先讓我們想像兩個情境：如果有天，我們想把一個五十公斤重的箱子搬起，是垂直將其向上拉起，還是將其推上一個斜坡比較省力？一般人遇到這個問題時，都會選擇斜坡，但卻鮮少有人去討論：為什麼是斜坡省力？

用力圖看斜面

首先，讓我們假設一個光滑無摩擦的斜面，其與水平面夾角為 $\theta$ 。在斜面上有一個質量 $m$ 的均勻木塊，那麼這個木塊在斜面上所受的重力，將會如下圖所示：

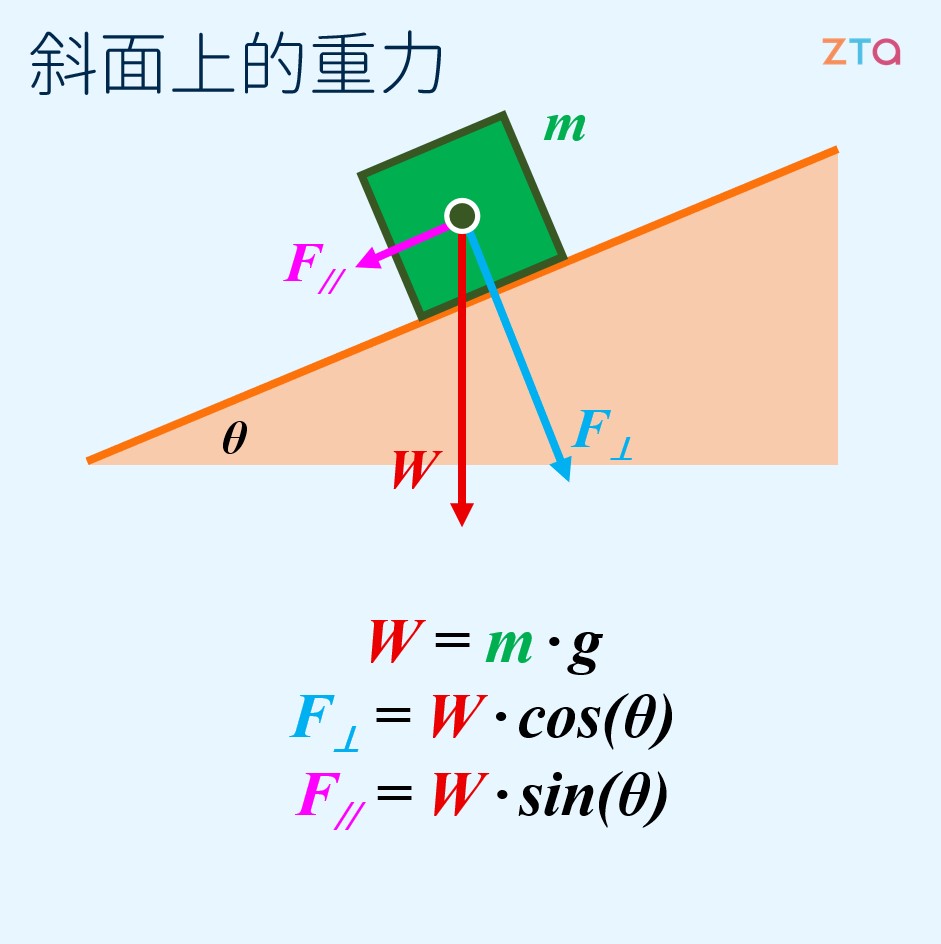
我們可以將木塊所受到的重力，分作與斜面垂直的 $F_\perp$，以及與斜面平行的 $F_{//}$。其中，$F_\perp$ 由斜面的正向力所支撐，而 $F_{//}$ 為向低處滑行的下滑力。

現在，我們將木塊置於斜面的底處，並且給它一個向上的能量讓它稍微動起來。接著，我們向木塊施力使其以等速度向斜面上運動，直到木塊到達斜面最高點為止。

整個過程中，木塊維持等速度運動，也就是說，木塊所受到的合力為 0。由此可知，我們將木塊上推的力 $F_{push}$ 等於木塊的下滑力，因此我們得到這樣的關係式：

$F_{push} = mg\cdot cos(\theta)$

現在，我們可以來回答剛剛的問題了：為什麼將木塊由斜面上推會比將木塊垂直向上拉來的省力？其實我們可以的重新思考這個問題—垂直上拉所施的力，就等於沿著 $\theta$ 等於 90 度的斜面上推所施的力，我們便能得到：

$F_\perp = mg\cdot sin(90) = mg$

因為 $sin(90)$ 等於 1，為 $sin$ 函數的極大值，因此當斜面傾角 $\theta$ 不等於 90 度時：

$F_{push}<F_{pushupwards}$

用作功看斜面

除了使用力圖之外，另一個可行的證明方法是使用作功。讓我們回到剛剛那個置於斜面上的木塊。現在，讓我們將木塊放置於斜面底部，並且將其以等速度上推，直到木塊抵達斜面頂端為止。

在這整段過程中，木塊的質量與速度均沒有改變，意味著過程中木塊沒有動能的變化。然而，木塊的高度改變了，也就代表著它有重力位能的變化。這個變化即是來自對木塊的施力所作的功。

接著，我們來探討一下斜推時與垂直上拉時，作功以及木塊的能量變化之間的關係。如下圖所示，我們假設兩個相同質量的木塊，分別以垂直與斜面被推上斜坡：

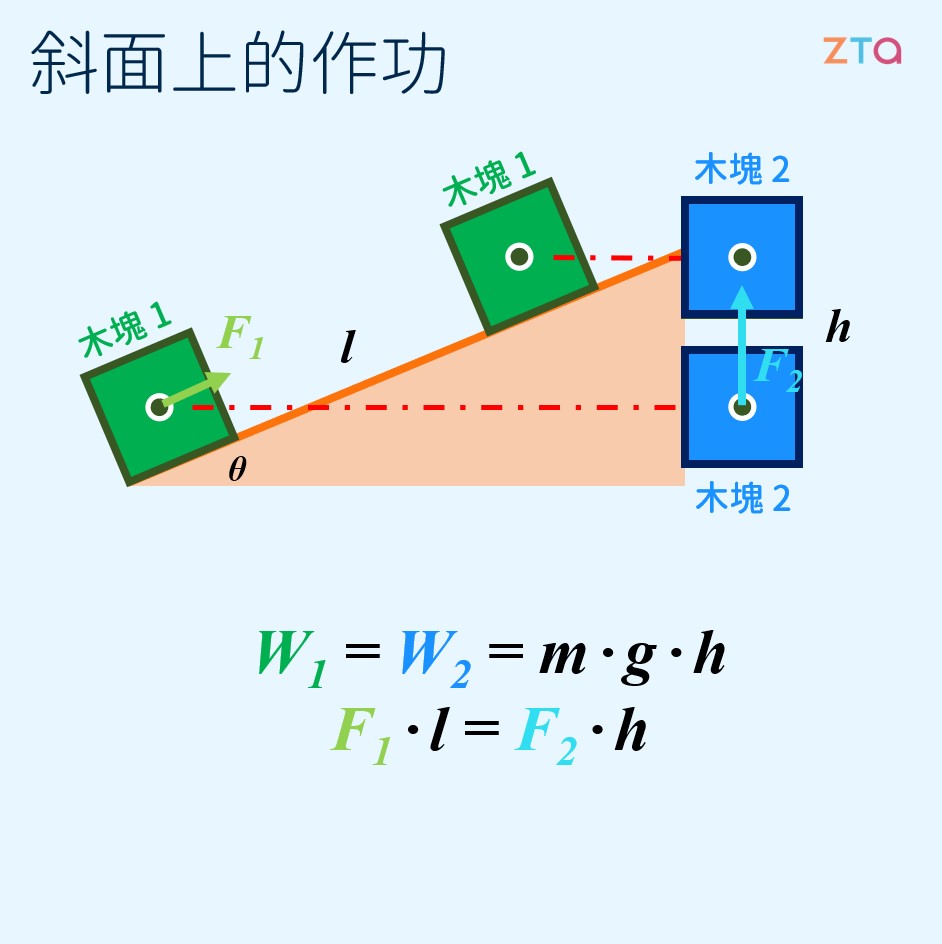
因為兩者的動能均沒有變化，因此變化的只有重力位能，而兩木塊最終的高度相同，可知兩者的位能變化相同，亦即所受到的作功相同。作功的定義如下：

$W= F\cdot S$

其中，$W$ 為作功，$F$ 為施力，$S$ 為位移量。在圖中，木塊 1 的位移量為 $l$，而木塊 2 的位移量為 $h$，而兩者所受到的作功 $W$ 相等，因此：

$F_1\cdot l = F_2\cdot h$

又因為：

$l>h$

我們可以得到結論：

$F_1< F_2$

這裡，我們能看到的是：用斜推的上斜面所需的力比垂直向上所需的力來的小，這也符合我們的生活經驗。另外，我們也能從中看到一個重要的物理概念：能量守恆。

儘管 $F_1$ 相較於 $F_2$ 來的小，兩者最終所作的功卻是相同的，這是因為 $F_1$ 必須經過比較大的位移，才能將木塊推向斜面的頂端。除此之外，我們還能藉此看到斜面「省力而費時」的特性。