機
器
人
微積分的介紹與意義
微積分──一個大家既熟悉又陌生的名字。微積分的可以是相當複雜的,但其背後的概念其實相當平易近人。在處理物理問題時,它是非常好用的工具。在這個章節裡,我們會利用大家熟悉的運動學,即為位移、速度與加速度,帶搭家一起認識微積分。
微分
我們都知道,一個以等速行進中的物體速率會等於「位移除以時間」,也就是單位時間內的位移:
其中, 代表位移,而 代表所經過的時間。然而,若該行進的物體並非以等速行進,那這個算式在取不同點時計算出的答案就會不同。那麼,我們要如何知道該物體在任一時間點時的速度呢?讓我們回到剛剛的算式:
讓我們思考一下,如果我們現在想要求得該物體在某個瞬間的速度,也就代表其所經過的時間 趨近於 ,那麼這個算式不就行不通了嗎?畢竟如果我們將 代入,就會有「除以 0」的問題產生。難道這代表我們永遠無法求得物體的瞬時速度嗎?
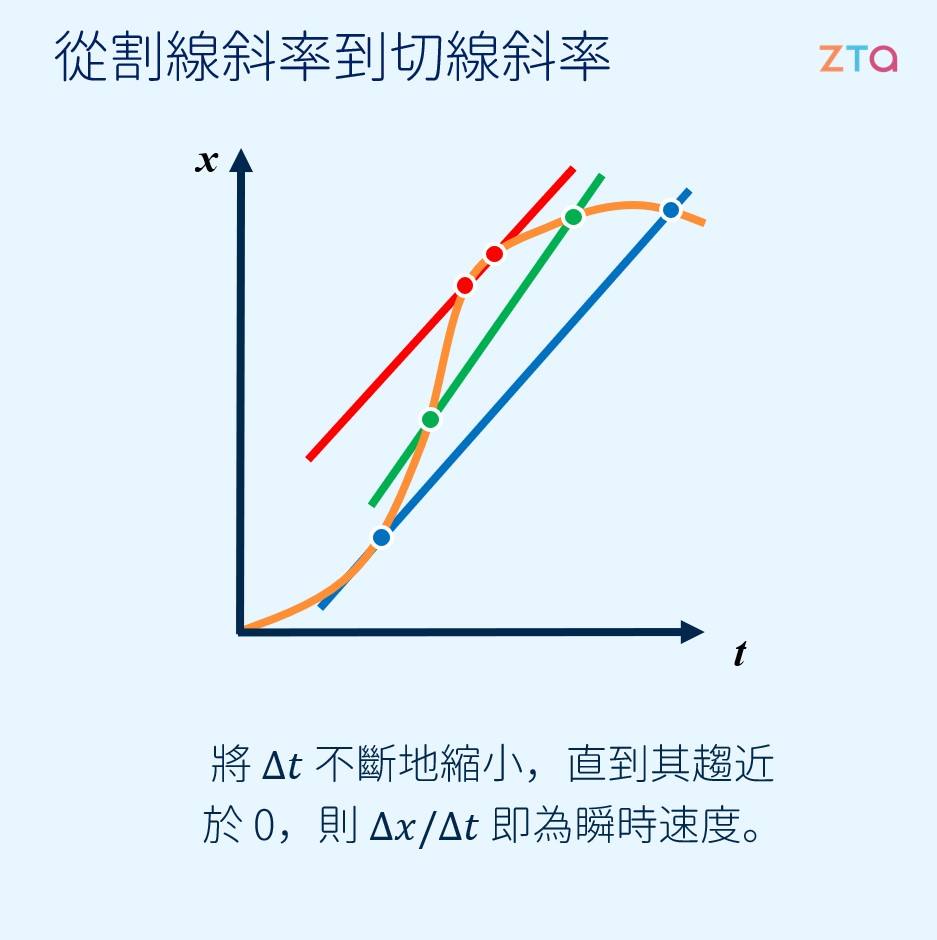
其實不然。讓我們由上圖想像一下,不斷地將 縮小,直到 趨近於 。此時再來觀察這個物體,會發現在極短時間內的物體運動可以視為等速運動。同時,我們也解決了「除以 0」的問題,因為我們是除以一個「趨近於 0」的數,就如下圖所示:

利用這個方法,我們就能利用 的算式算出某個特定時刻的物體速率:利用極短時間內的位移量除以時間變化量。這個時候,我們就將 記為 ,其中的 這個符號稱為導數(derivative)。因此,物體運動時,每個瞬間的速度都可以用這個式子來表示:
其中, 是速度, 是很短時間內的位移量, 則是經過的那段很短的時間。因此我們會說,「速度就是位移對時間的微分」。
上面說了這麼一大堆,目的只是要賦予這個式子物理意義,也是在處理物理問題時能夠列出式子的關鍵。「速度是位移對時間的微分」,意義是極短時間內物體走的一小段位移 除上一小段時間 ,而在數學上這樣的定義其實就是大家所熟悉的切線斜率。
積分
我們現在已經知道物體運動的速率:
經過移項之後可以得到:
接著,讓我們回想一下, 表示的是很小的一段位移,而 表示的是很小的一段時間。 也就是說,在極短時間的時間之內,物體前進的距離 會等於速度 乘上 。咦?這不就是等速度運動的公式 嗎?或許你會想問:如果物體不是以等速度前進,那這個式子不就不能套用了嗎?
其實不然。在上面在微分的部分我們已經提到過,如果將時間縮減的極短,那麼就算是變速度運動的物體,速度的改變量會因為太小而可以忽略,因此可以將物體視為等速度運動。
那如果要求的不是極短時間行進的距離呢?為了解決這個問題,我們的想法是分別求每一段極小的時間 內所行進的距離 ,最後再將它加起來,就能得到總行進的距離了,如圖所示:
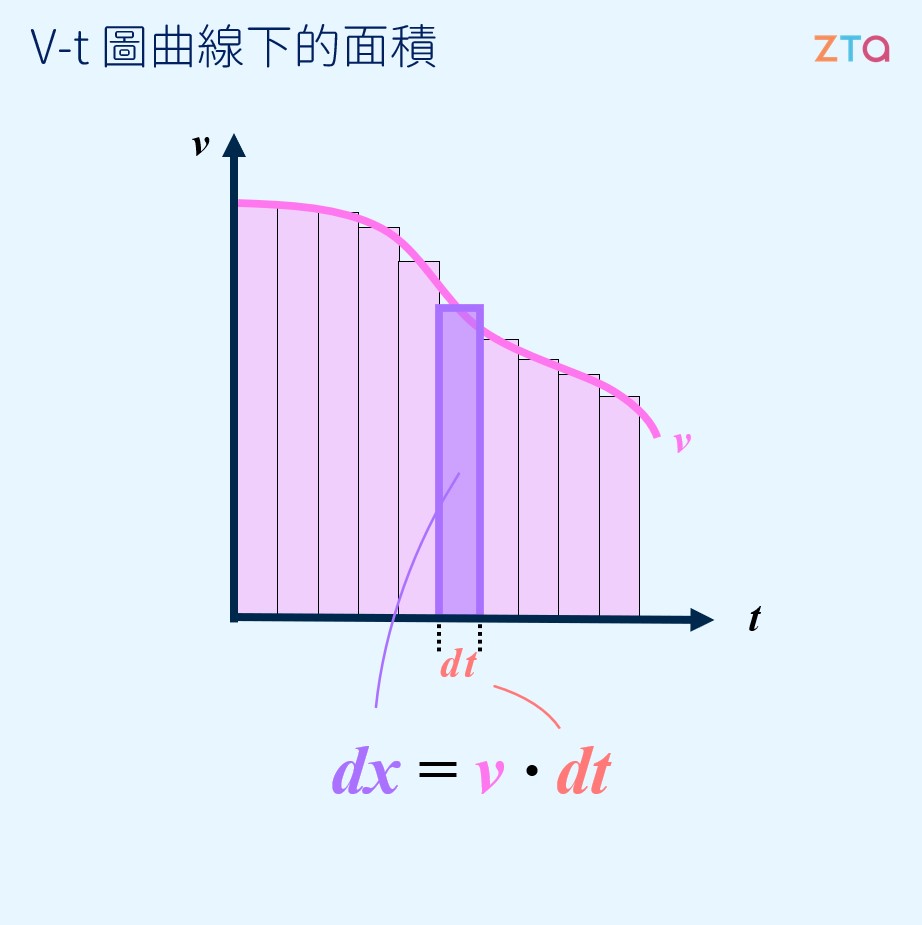
然而,由於 極小,要加總的數量非常多,處理起來相當麻煩。因此,我們能夠運用積分來解決以上的問題。讓我們重新寫下剛才的式子:
接著,同時在式子兩側加上積分符號 :
在積分符號上下的 與 代表的是積分的上下限,也就是指從 到 的範圍進行積分。等式右邊的 與 也是同樣的概念。這裡要注意的是, 與 必須是代表同一個狀態下的參數,也就是說,當位置為對時間的函數為 時,必須滿足 ,而 與 也是同理。
由上述可知,位移是速度對時間的積分,亦即,一個物體的位移,會等於將其每一小段時間 中行進的距離 的總和。在數學上,其實我們所求的,就是大家所熟悉的函數曲線下面積。