拋物線運動
我們都有過這種經驗:將籃球投向籃框、將鉛筆袋拋給坐在教室對面的同學、將棒球丟向捕手。但是你有沒有認真去思考過,這些東西有什麼共通點呢?答案是:它們都會向下掉落。這種物體在飛行過程中向下掉落的運動模式,稱為拋物線運動。
等加速度運動
假設我們將一顆球,以某一個角度向前丟出,那麼這顆球在向前飛行的同時,將會先向上飛,到達一定的高度後向下墜落,最後落地於我們前方某處。假設這顆球在飛行路徑中不受任何空氣阻力的影響,那麼它就只被地心引力影響。
也就是說,球從一開始的向上飛,到最後的向下掉落,都只受到同樣的力影響,亦即它只受到同樣的加速度影響。而在前面的章節中,我們對 重力加速度 有了基本的概念,將概念運用在此,我們可以說:「物體在飛行的過程中,一直受到重力加速度 g 的影響。」
g=9.81m/s2
垂直與水平速度
我們都知道,在計算向量的過程中,可以將向量拆解成多個向量的相加。在討論拋物線運動時,我們將物體運動速度分別分為垂直速度與水平速度來討論。假設現在我們已知物體的初速度為 V0,那麼我們便能得到:
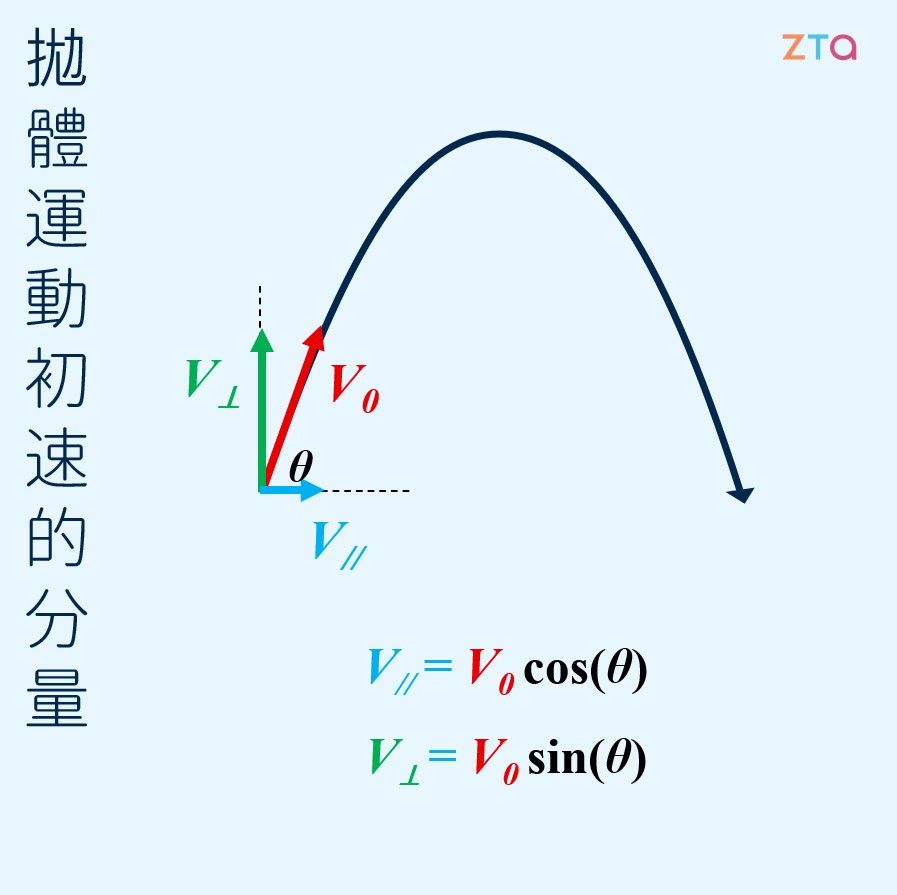
而我們也知道,對於一個拋體而言,它在飛行的路徑中無時無刻都受到重力加速度 g 的影響,如下圖所示:
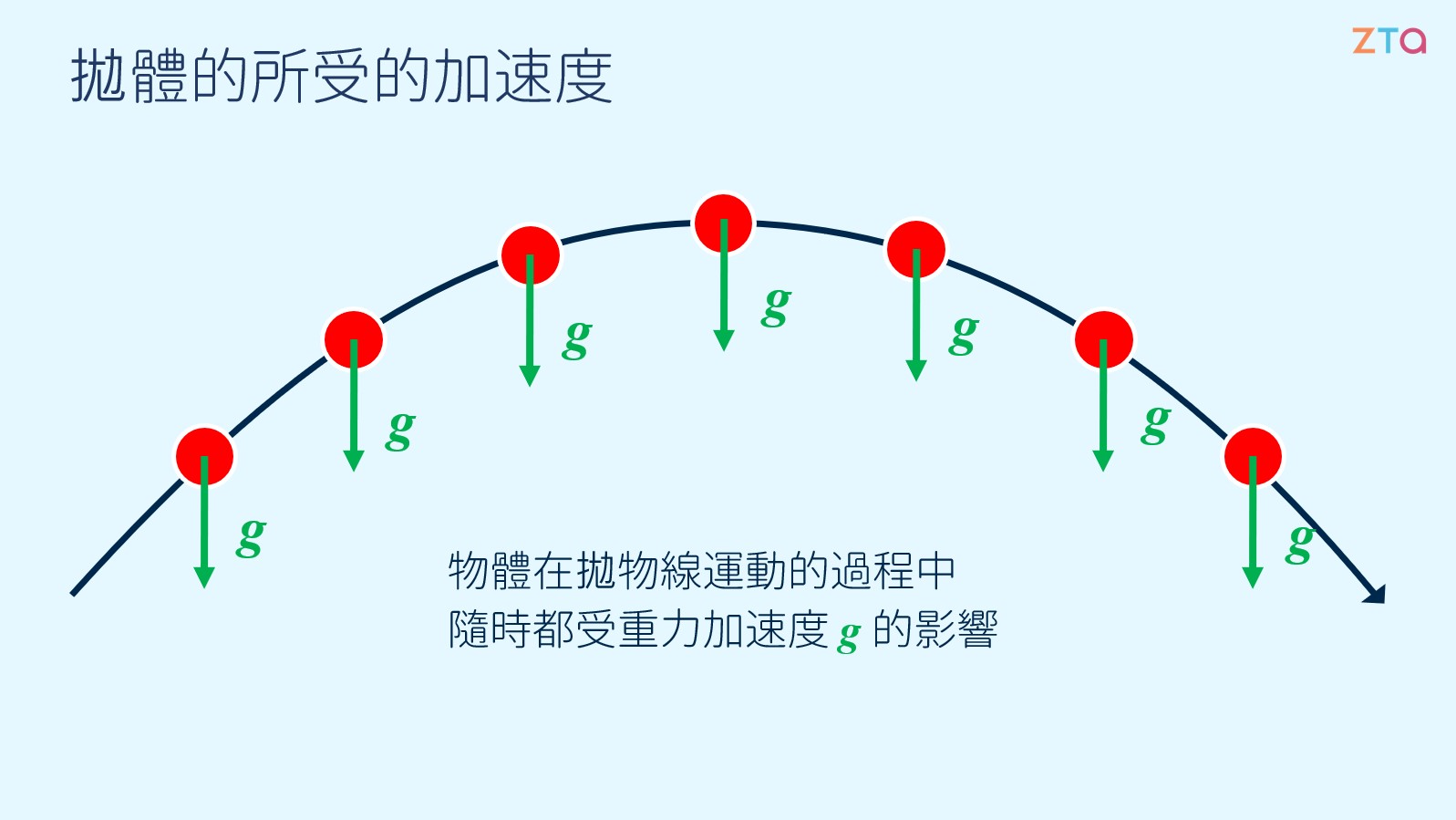
因為鉛直方向的速度所受的加速度,在飛行的整段過程中都是重力加速度 g,因此鉛直方向呈現等加速度運動,於是我們可以得到在物體落地前的任意時間點,其鉛直速度與時間的關係式:
V⊥=V0⋅sin(θ)−gt
而因為重力加速度並不影響水平速度,因此飛行的過程中,水平速度不變:
V//=V0⋅cos(θ)
最高點高度
拿剛剛向前拋球的例子來看,我們該如何計算那顆球可以到達的最高點呢?既然我們已經知道了初速度 V0 以及其與地面的夾角 θ,那麼我們就可以開始計算了!
首先,讓我們思考一下,在什麼樣的情況下,才代表球達到其最高高度?其實這很簡單:只要球不再具有向上的鉛直速度,就代表它已經達到最高點了。也就是說,當鉛直速度 V⊥ 受到重力加速度 g 而變成 0 的那一刻,就代表球達到了最高點。又因鉛直方向為等加速度運動,我們可以得到:
V⊥−gt=0
解方程式後,我們得到到達最高點的時間 t:
t=gV⊥
接著,因為鉛直方向為等加速度運動,且其加速度大小為重力加速度 g,我們便能使用這個式子,其中 h 代表高度:
h=21gt2
帶入剛剛求得,到達最高點所需的時間 t,我們便能獲得最大高度:
hmax=21gt2
=21g⋅(gV⊥)2=2gV⊥2
=2gV02⋅sin2(θ)
水平射程
假設剛剛那顆球是從地面向上拋出,那麼要怎麼知道球會落在距離起始點多遠的地方呢?讓我們想想看:因為球最後落在相同的水平面,而且過程中水平速度維持不變,因此只要將水平初速乘上飛行總時間即可求得落地的距離。
而我們已知飛行的初速度是 V0,也就是說,水平初速度是 V0⋅cos(θ),現在唯一缺乏的條件,就是飛行的總時間了。現在,讓我們思考飛行的時間應該怎麼計算:因為飛行路徑呈現拋物線,因此路徑以最高點為對稱軸左右對稱—從地面到最高點所需的時間,等於從最高點回到地面的時間。
我們從剛剛的推導得到,到達最高點所需的時間:
th,max=gV0⋅sin(θ)
整段路徑所需的時間:
tdrop=g2V0⋅sin(θ)
接下來,因為物體在水平方向呈現等速度運動,我們只需要將初始的水平速度乘上飛行的總時間,就可以得到物體落地點與其出發點的距離了:
D=V//⋅tdrop
=V0⋅cos(θ)⋅g2V0⋅sin(θ)
將式子化簡,並且使用三角函數的兩倍角公式:
sin(2θ)=2sin(θ)cos(θ)
我們便能得到最終的算式:
D=gV02⋅sin(2θ)
最大水平射程
在瞭解了以上的公式之後,我們不禁想問:要以什麼樣的角度拋射才可以達到最大的水平射程呢?一般人會很直覺性地回答:45 度。是的,這個答案是正確的,但是要怎麼證明 45 度可以飛的最遠呢?
我們只需要使用剛剛的水平射程公式:
D=gV02⋅sin(2θ)
在相同初速度的情況下,如果我們想要將射程 D 變到最大,就表示 sin(2θ) 需要達到最大值。而具有一些三角函數背景的我們都知道,sin(90°) 時會達到最大值 1,因此若要具有最大射程,則:
2θ=90∘
⇒θ=45∘
軌跡方程式
最後,讓我們來看看拋體的軌跡方程式。如果現在,我們被要求要在 x-y 平面上畫出一個拋物線的軌跡,並且使用方程式來描述它,那麼我們要怎麼做呢?我們可以將鉛直與水平方向分開來討論。
因為鉛直方向是加速度為 g 的等加速度運動,而水平方向則是等速度運動,我們可以得到水平與鉛直(x 和 y)位置對時間的關係式:
x=V0⋅cos(θ)⋅t
y=V0⋅sin(θ)⋅t−21gt2
我們的目標是求出 x 和 y 間的關係式,因此我們要將 t 消去。先解 t:
t=V0⋅cos(θ)x
接著,將 t 代入 y 對 t 的關係式:
y=V0⋅cos(θ)V0⋅x⋅sin(θ)−2g⋅V02⋅cos2(θ)x2
化簡之後即得拋體運動的軌跡方程式:
y=tan(θ)⋅x−2V02⋅cos2(θ)gx2

